Parrondo’s Paradox Explains How Two Losing Strategies Combined Can Win

Mathematical Paradox Shows How Combining Losing Strategies Can Lead to Victory

TO Manon Bischoff edited by Daisy Yuhasz

In 1996, Spanish physicist Juan Parrondo made a discovery. incredible discovery: Sometimes two games, each of which ends in a loss individually, can be combined into a winning strategy. This paradox is not just a mathematical curiosity—it is scientifically useful. This helps explain The varied life history of slime molds and can contribute to the creation of new cancer treatment strategies.

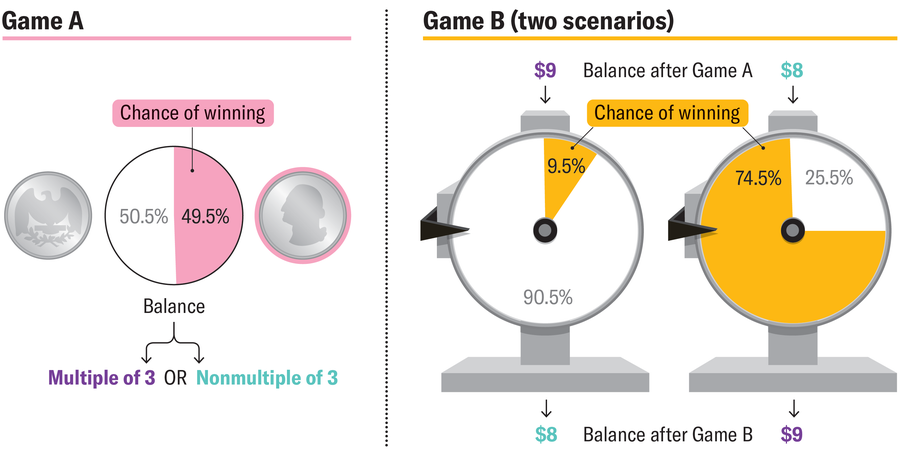
To understand this paradox, we need to imagine a situation in which you are playing two games with very specific parameters. For example, let's imagine that the first game “A” involves tossing a coin. The coin in this case has a slightly changed weight distribution, so that it will fall predominantly on one side with a probability of 50.5 percent. Now let's assume that Game A is somewhat rigged so that I win if he lands on the preferred side and you win if he lands on the other side. So you only have a 49.5 percent chance of winning, in which case I'll give you $1; otherwise you will pay me the same amount.

If you play Game A against me many times, you will inevitably suffer big losses because you will have to pay me an average of one cent per game. (We can quickly calculate this by taking the probability of you winning and subtracting the probability of me winning: 0.495 – 0.505 = –0.01.)

---

About supporting science journalism

If you enjoyed this article, please consider supporting our award-winning journalism. subscription. By purchasing a subscription, you help ensure a future of influential stories about the discoveries and ideas shaping our world today.

---

Then there is a second, more difficult game “B”, in which you need to spin two wheels of fortune. In this game you will be able to spin this or that depending on how much money you have at the moment. If your available capital for the game (based on how you played A) is divisible by 3, then you spin the wheel of fortune, which gives you only a 9.5 percent chance of winning. On the other hand, if your capital is not divisible by 3, you get better odds: you spin another wheel, which gives you a 74.5 percent chance of winning.

Now things get interesting.

Two games you can only lose

In Game B, the bet is again $1. On average you will lose 87 cents per spin.

Let's dive into this. You can assume that a third of the time you will be spinning the wheel that is unfavorable to you, and two-thirds of the time you will be spinning the other wheel. But this is not true because your money does not fluctuate evenly. For example, if you have $9, you will turn the unfavorable wheel and most likely lose, leaving you with only $8. However, if you play the game again with this amount, you will start spinning the wheel that is more profitable for you and you will have a better chance of winning. So you will get $9 again.

So the chance that you have an amount of money that is a multiple of 3 is well over one third. Using a complex procedure known as a Markov chain, you can calculate that your overall probability of winning Game B is only 49.565 percent, and your expected profit per round is negative: 0.49565 – 0.50435 = –0.0087.

A paradox appears

If you are smart, you will not play against me in either Game A or Game B. In both cases, you will definitely lose in the long run. But Parrondo realized that a mixed strategy can pay off: By alternating between games A and B, you can actually win overall.

For example, if you always play two rounds of Game A and then two rounds of Game B, you will win an average of 1.48 cents per round. Or, if you follow each Round A with two Rounds B, you'll earn an average of 5.8 cents per round. So in the long run you will profit in both cases.

As Parrondo discovered, there are more combinations of A and B that have positive expected value for you than the other way around. This way you come out a winner even if you randomly choose whether to play A or B each round (for example, letting a fair coin decide). In this case, your average win will be 1.47 cents per round.

How is this possible? The key to Parrondo's paradox is that two games A and B can influence each other because game B depends on the money you have at the moment, and that amount fluctuates as you play game A. Therefore, A and B can no longer be considered independent games. This is the essence of Parrondo's paradox. If Game B were modified so that, for example, the value of the die determined which wheel of fortune you would spin, the paradox would disappear since the two games would be completely independent of each other.

Application of Parrondo's Paradox

Since Parrondo's astonishing publication in 1996, numerous articles have appeared on this topic. In 2017, two computer scientists demonstrated that this paradox may explain the different life strategies of slime molds, which can alternate between solitary nomadic life and stationary colony life.

In some situations, it is more profitable for these creatures to gather together and form colonies, rather than exist as solitary wanderers. But these collective living conditions also cannot survive in the long term: organisms exploit the environment, and eventually resources begin to be depleted. Adherence to one strategy will inevitably lead to death, but a mixed strategy offers a solution: organisms temporarily become mobile again while the environment in a certain area is restored.

Computational physicist Jian-Yue Guan of Lanzhou University in China and her colleagues presented another application of Parrondo's paradox. in an article published in Physical Review E in August 2025. For many types of cancer, two different approaches to chemotherapy are used. Patients are either given the maximum tolerated dose at intervals or are treated with a continuous low dose. The disadvantage of the first strategy is that some tumor cells develop resistance and therefore do not respond to the drug. In the second strategy, the concentration of the drug is not always high enough to completely destroy all cancer cells.

Using computer simulations, the researchers demonstrated that switching between the two treatment approaches at a set time could lead to better results even without detailed monitoring—just as randomizing A and B was beneficial in the lottery example. Whether this theoretical approach can actually be applied to cancer medicine requires further study. Guan and her team plan to test their ideas using in vitro studies.

This article originally appeared in spectrum of science and reproduced with permission.