Earlier today I asked a riddle that is extremely difficult to answer unless you are a bubbler.
Four cities
The four cities are located at the corners of the square, as shown below:
Which road system connects all four cities using the shortest total road length?
What perhaps seems like the right answer is a network in which opposing cities are connected by straight lines.
In fact, the minimal network is shown below and reduces the length of solution X by about 4 percent. The three angles at the points of intersection are equal, 120°.
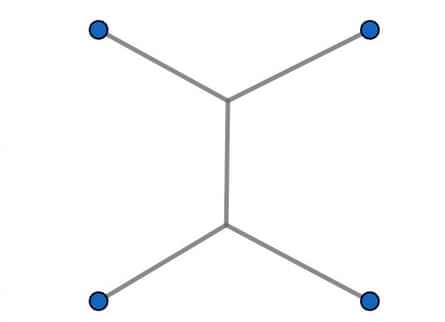
Theoretical proof that this pattern is minimal requires advanced calculus. But you can find an easier answer using soap bubbles.
If you make a plastic model of a puzzle (a sandwich, where the “bread” is two pieces of transparent flat material, and the “filling” is four short dowels of equal length, located at the corners of the square) and dip it in soapy water, bubbles will form around the dowels, representing the answer. Here's a video of how it works, presented by James Grime.
I like this problem because it is one of the clearest illustrations of how Nature effortlessly solves optimization problems that would otherwise require a lot of thought.
I suggested that the pattern resembles a geometric figure that appears in the real world in a very familiar setting. If all angles at the intersection points are equal to 120°, we get hexagons – this is Nature's answer to the question of how to store honey most efficiently. Sweet!
For further reading about the science of bubbles, I recommend this classic 1976 article. Soap Movie: Analog Computer from an American scientist.
I've been doing puzzles here on Mondays since 2015. I'm always on the lookout for great puzzles. If you would like to offer one, write to me.








